Verifiche muratura per carichi laterali: caso statico

Le verifiche a pressoflessione per carichi laterali hanno lo scopo di controllare che le eccentricità dei carichi applicati, al di fuori del piano medio della parete, siano tali da non compromettere la stabilità del muro. Si tratta di una verifica di tipo locale, effettuata sulla singola muratura portante, che mira al controllo delle sollecitazioni di scarico dei solai, delle travi e di eventuali pareti sovrastanti quella in esame.

L’analisi è condotta nell’ipotesi di conservazione delle sezioni piane e resistenza a trazione nulla della muratura.

La procedura consiste essenzialmente, in una verifica a sforzo normale centrato, assumendo per la muratura una resistenza a compressione ridotta, per portare in conto l’effetto delle eccentricità trasversali dei carichi e dei fenomeni del secondo ordine.

Nella procedura semplificata, lo sforzo normale resistente N_Rd della parete, si assume pari a:

$N_{Rd}=\phi\cdot f_{d}\cdot A$

in cui Φ è il coefficiente di riduzione della resistenza di progetto del materiale (leggi di più sui coefficienti di sicurezza da utilizzare per le verifiche) f_ddel materiale, calcolato di funzione dell’eccentricità e della snellezza λ della parete. A è l’area della sezione trasversale della parete (lunghezza B X spessore t)

Eccentricità dei carichi verticali

I carichi verticali agenti nella sezione di testa della parete inferiore (si veda la figura successiva), di sezione trasversale pari a t₂xB, sono caratterizzati da una eccentricità e_S totale che può essere calcolata come:

$e_{s}=e_{s1}+e_{s2}$

$e_{s1}=\frac{N_{1}\cdot d_{1}}{N_{1}+\sum N_{2}};e_{s2}=\frac{\sum N_{2}\cdot d_{2}}{N_{1}+\sum N_{2}}$

Figura 1 – Schema parete nel piano trasversale

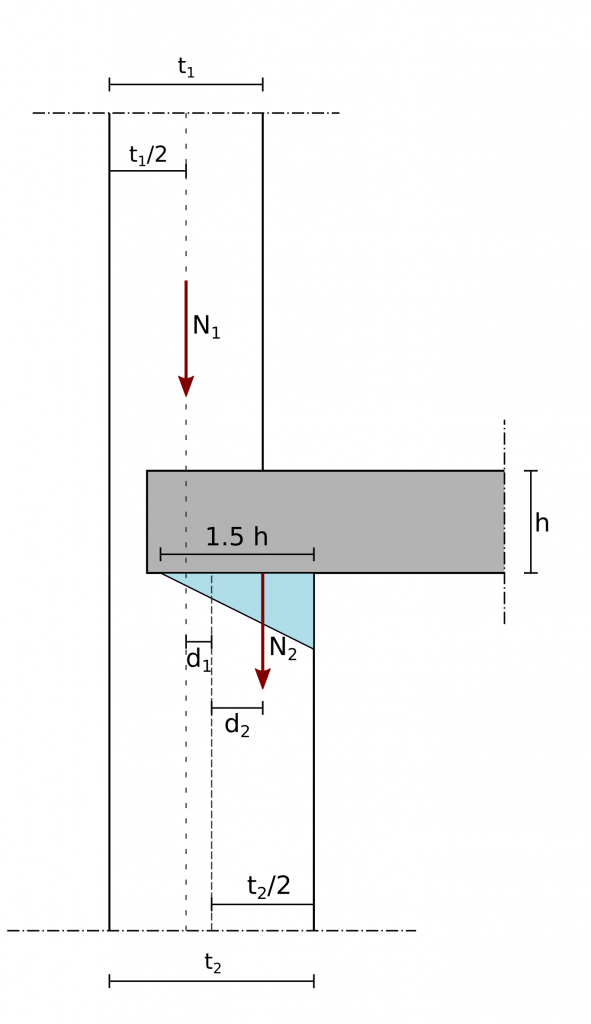
dove:

N₁ è il carico trasmesso dal muro superiore;
N₂è il carico trasmesso dal solaio il cui peso grava sul muro da verificare;
d₁ e d₂ sono rispettivamente l’eccentricità di N₁ e di N₂rispetto al piano medio del muro da verificare.

Il calcolo dell’eccentricità viene effettuato nell’ipotesi che il peso del singolo pannello sia centrato rispetto al pannello stesso e che il solaio scarichi il proprio peso sul muro con una distribuzione di tensioni triangolare in una zona di lunghezza pari a 1.5 volte la sua altezza.

Eccentricità accidentale

Per quanto riguarda l’eccentricità accidentale e_a, connessa alla tecnologia di costruzione degli edifici, si assume:

$e_{a}=\frac{H}{200}$

con H altezza interna di piano.

Eccentricità dei carichi orizzontali

I carichi orizzontali che agiscono in direzione ortogonale al piano della muratura (ad esempio l’azione del vento, assunta distribuita lungo la parete), nell’ipotesi che la parete sia schematizzata come incernierata nelle sezioni di estremità, sono caratterizzati da un’eccentricità e_v, che si valuta come:

$e_{v}=\frac{M_{V}}{N}$

dove:

M_V è il massimo momento flettente dovuto alle azioni orizzontali, che si attinge in mezzeria e vale qH²/8, essendo q il carico distribuito lungo l’altezza H della parete.
N è il valore dello sforzo normale nella sezione di verifica.

CALCOLO DELLA RESISTENZA

Per quanto riguarda le verifiche, è necessario condurle nelle sezioni di estremità del muro e nella sezione di momento massimo. Nel primo caso, come regolamentato dalle NTC 2018, l’eccentricità che si considera per il calcolo vale:

$e_{1}=|e_{s}|+e_{a}$

nel secondo invece:

$e_{2}=\frac{e_{1}}{2}+|e_{v}|$

Sulla base dei valori di e₁ e e₂ si calcoleranno due valori di sforzo normale resistente da confrontare con quelli sollecitanti.

Il primo passo per procedere alle verifiche è definire: il coefficiente di eccentricità m:

$m=\frac{6e}{t}$

la snellezza della parete λ:

$\lambda=\frac{h_{0}}{t}\leq20$

Essendo h₀ l’altezza libera di inflessione definita sulla base del fattore di efficacia del vincolo ρ:

$h_{0}=\rho\cdot H$

Per la determinazione di ρ le NTC prescrivono di assumere: “il valore 1 per muro isolato, e i valori indicati nella Tab. 4.5.IV (riportata di seguito), quando il muro non ha aperture ed è irrigidito con efficace vincolo da due muri trasversali di spessore non inferiore a 200 mm, e di lunghezza l non inferiore a 1/5 h, posti ad interasse a”.

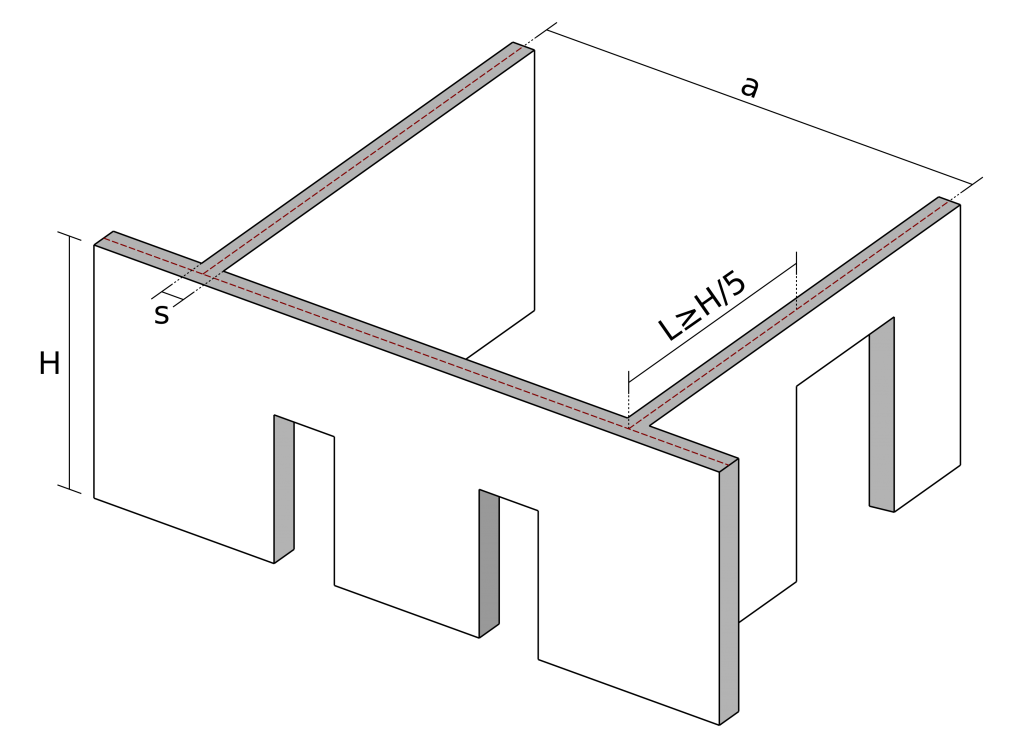
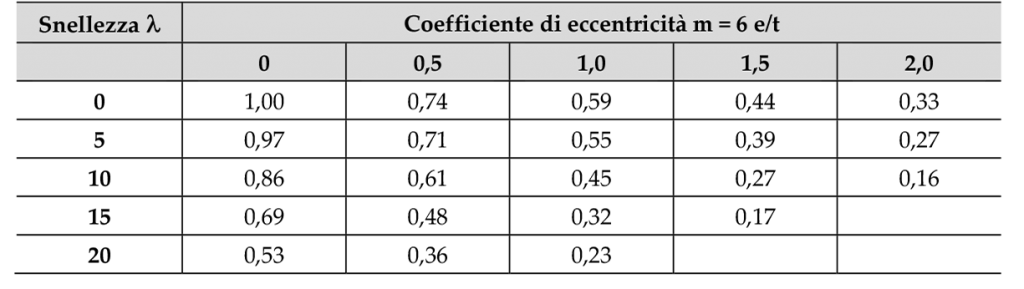
Noti i valori di m e λ è possibile ricavare il valore di Φ dalla tabella seguente e di conseguenza il valore dello sforzo normale resistente da confrontare con quello sollecitante, attraverso la relazione:

$N_{Rd}=\phi\cdot f_{d}\cdot A$

Scopri di più sulle soluzioni software per l’analisi lineare e non lineare di costruzioni in muratura. Scrivi a comunicazione@soft.lab.it o telefona allo 0824 87 43 92.

Resta sempre aggiornato e segui le pagine Facebook, Linkedin, Instagram e YouTube per non perdere le ultime novità!

Tags calcolo strutturale muratura NTC 2018

Verifiche muratura per carichi laterali: caso statico

Eccentricità dei carichi verticali

Eccentricità accidentale

Eccentricità dei carichi orizzontali

CALCOLO DELLA RESISTENZA

Lascia un commento Annulla risposta

SOFTWARE PER IL CALCOLO STRUTTURALE E LA GEOTECNICA