La spinta del terreno sulle opere di sostegno

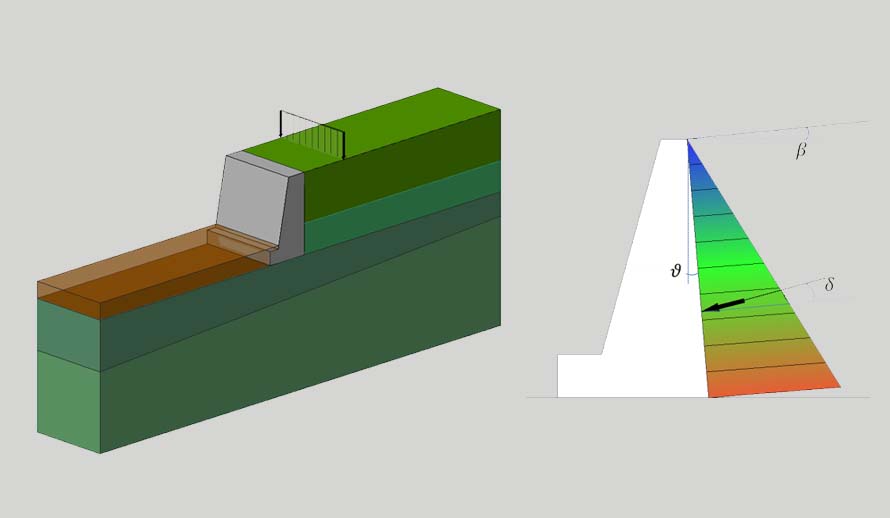
Uno dei problemi classici dell’ingegnere geotecnico riguarda la valutazione della spinta del terreno sulle opere di sostegno. La letteratura scientifica presenta diverse teorie a seconda delle ipotesi di superficie assunta; nel caso di superficie di scorrimento piane i più noti sono la Teoria di Rankine, il Metodo di Coulomb e il Metodo di Mononobe-Okabe mentre nel caso di superfici di scorrimento curve si ha Mistilinea (cerchio + retta), Spirale logaritmica (Caquot e Kerisel – Kerisel e Absi). Di seguito sono riportate le equazioni e le ipotesi per il calcolo della spinta attiva e passiva indotte da uno strato omogeneo di terra spingente, secondo le teorie più accreditate, utilizzate nel software per il calcolo e la verifica dei muri di sostegno Monolith 3 e nel software per il calcolo lineare e non lineare di paratie Bulk.

Spinta del terreno in assenza di sisma: la teoria di Coulomb

Nel caso in cui non si consideri il sisma, il calcolo della spinta del terreno viene eseguito con riferimento alla teoria di Coulomb meglio nota come teoria del cuneo di rottura, nella quale si considera l’equilibrio limite delle forze agenti sul cuneo di spinta, assumendo la superficie di scorrimento piana e inclinata rispetto all’orizzontale. La teoria di Coulomb, estesa analiticamente da Muller-Breslau ai casi più generali, è basata sulle seguenti ipotesi:

• terreno isotropo e omogeneo;
• superficie di rottura piana;
• superficie del terrapieno di riempimento piana;
• resistenza per attrito uniformemente distribuita lungo la superficie di rottura;
• la superficie del paramento interno del muro piana e inclinata di un angolo;
• la presenza dell’attrito fra muro e terreno δ.

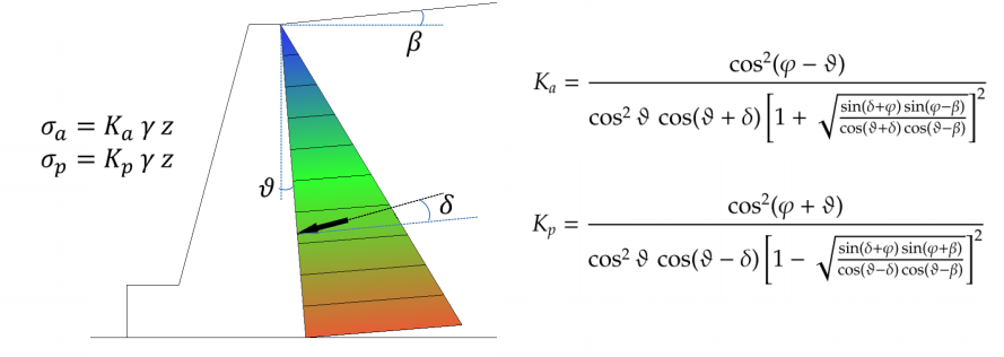
In cui abbiamo:

• K_a coefficiente di spinta attiva;
• K_p coefficiente di spinta passiva;
• ϕ l’angolo di attrito (o di resistenza a taglio) del terreno;
• δ l’angolo di attrito fra terreno e paramento virtuale;
• β l’angolo formato dall’estradosso del terrapieno con l’orizzontale;
• ϑ l’angolo formato dal paramento virtuale con la verticale.

Nel caso in cui δ=β=ϑ=0 (paramento virtuale verticale liscio e terrapieno con superficie orizzontale) le equazioni sopra riportate coincidono con quelle della teoria di Rankine le cui ipotesi sono:

• terreno isotropo e omogeneo;
• superficie di rottura piana;
• superficie del terrapieno di riempimento piana;
• resistenza per attrito uniformemente distribuita lungo la superficie di rottura;
• superficie del paramento interno del muro piana e verticale;
• assenza di attrito muro-terreno.

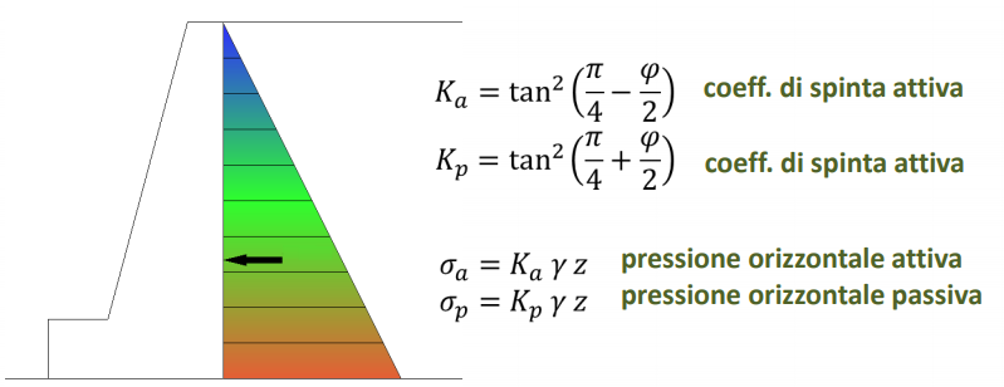
Spinta del terreno sotto sisma: il metodo di Mononobe-Okabe

Nel caso in cui si consideri la spinta del terreno sotto l’azione sismica viene utilizzato il metodo di Mononobe-Okabe. Le NTC 2018 al §7.11.6 ammettono l’utilizzo dei metodi pseudostatici e questo è ancor di più esplicitato al § 7.11.6.2.1 e §7.11.6.3.1.

Le ipotesi alla base del Metodo di Mononobe-Okabe (metodo pseudostatico) sono:

• muro abbastanza lungo da poter trascurare gli effetti locali alle estremità;
• muro libero di traslare orizzontalmente o ruotare attorno al piede in modo tale da mobilitare le condizioni di spinta attiva;
• terrapieno omogeneo e privo coesione;
• superficie del terrapieno piana (non spezzata o irregolare);
• eventuale sovraccarico applicato al terrapieno uniforme ed esteso oltre il cuneo di rottura;
• superficie di rottura del terreno piana e passante per il piede del muro;
• effetti inerziali del muro trascurabili;
• nessun rischio di liquefazione.

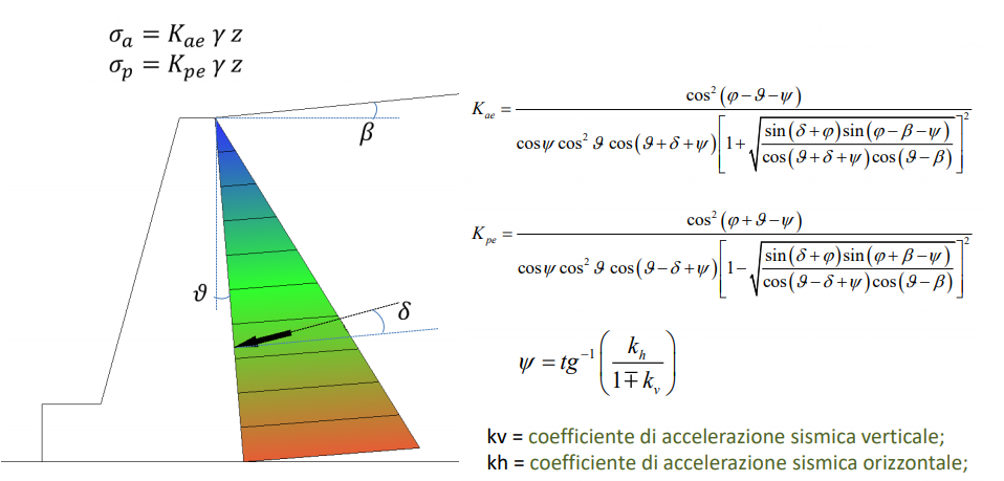
In cui:

• ψ = tan⁻¹ [k_h/(1+k_v)] l’angolo sismico
• k_h il coefficiente di accelerazione sismica orizzontale
• k_v il coefficiente di accelerazione sismica verticale
• ϕ l’angolo di attrito (o di resistenza a taglio) del terreno
• δ l’angolo di attrito fra terreno e paramento virtuale
• β l’angolo formato dall’estradosso del terrapieno con l’orizzontale
• ϑ l’angolo formato dal paramento virtuale con la verticale

I valori dei coefficienti sismici vengono valutati mediante le espressioni fornite al §7.11.6.2.1 NTC 2018.

   

   

   

• S_s è il coeffciente che tiene conto dell’effetto dell’amplificazione stratigrafica
• S_T è il coeffciente che tiene conto dell’effetto dell’amplificazione topografica
• ag è l’accelerazione orizzontale massima attesa sul sito di riferimento rigido.
• β _m è il coefficiente di riduzione dell’accelerazione massima attesa al sito

Per le NTC 2018 invece tali valori sono:

   

Rispetto alla nuova norma le NTC 2008 invece fanno riferimento alla tabella 7.11.II:

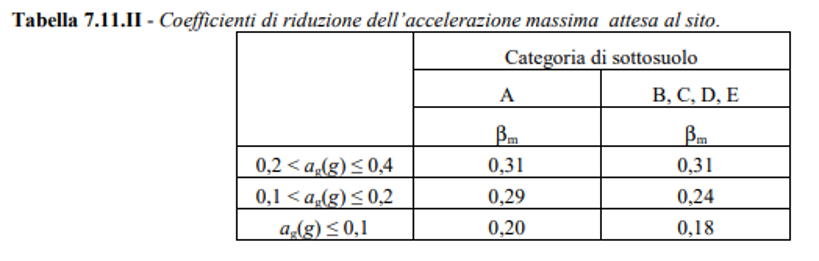
Muri vincolati al piede

Un ulteriore precisazione occorre farla per la spinta del terreno sotto sisma nel caso di muri vincolati al piede. Nel caso di muri di sostegno non liberi di traslare o di ruotare intorno al piede (muri tirantati o fondati su pali), le spinte in condizioni sismiche sono maggiori di quelle valutate nel caso di muri liberi (Mononobe-Okabe). A tal proposito, al §7.11.6.2.1 delle NTC 2018 viene indicato solo il punto di applicazione dell’incremento di spinta, fissato a metà altezza del muro, ed il valore di k_h che viene posto, senza alcun fattore riduttivo, pari a:

   

con β _m pari a 1.

Acquista Monolith 3 il software per il calcolo dei muri di sostegno e Bulk il software per il calcolo lineare e non lineare di paratie. Sei interessato a entrambi? Scopri i vantaggi del Geotecnica Pack.

Vuoi provare senza vincoli? Scarica la versione Time Edition di Monolith 3 e Bulk e scopri i vantaggi della soluzione a tempo per 30 gg a soli 59 € IVA inclusa.